Skip to contents

Extinction Risk Estimation for a Density-Independent Model

ext_di.Rd

Estimates demographic parameters and extinction probability under a density-independent (drifted Wiener) model. From a time series of population sizes, it computes MLEs of growth rate and environmental variance, then evaluates extinction risk over a horizon \(t^{\ast}\). Confidence intervals are constructed by the \(w\)-\(z\) method, which achieve near-nominal coverage across the full parameter space.

Usage

ext_di(
  dat,
  ne = 1,
  th = 100,
  alpha = 0.05,
  unit = "years",
  qq_plot = FALSE,
  formatted = TRUE,
  digits = getOption("extr.digits", 5L)
)

Arguments

dat

Data frame with two numeric columns: time (strictly increasing) and population size. Column names are not restricted.

ne

Numeric. Extinction threshold \(n_e \ge 1\). Default is 1.

th

Numeric. Time horizon \(t^{\ast} > 0\). Default is 100.

alpha

Numeric. Significance level \(\alpha \in (0,1)\). Default is 0.05.

unit

Character. Unit of time (e.g., "years", "days", "generations"). Default is "years".

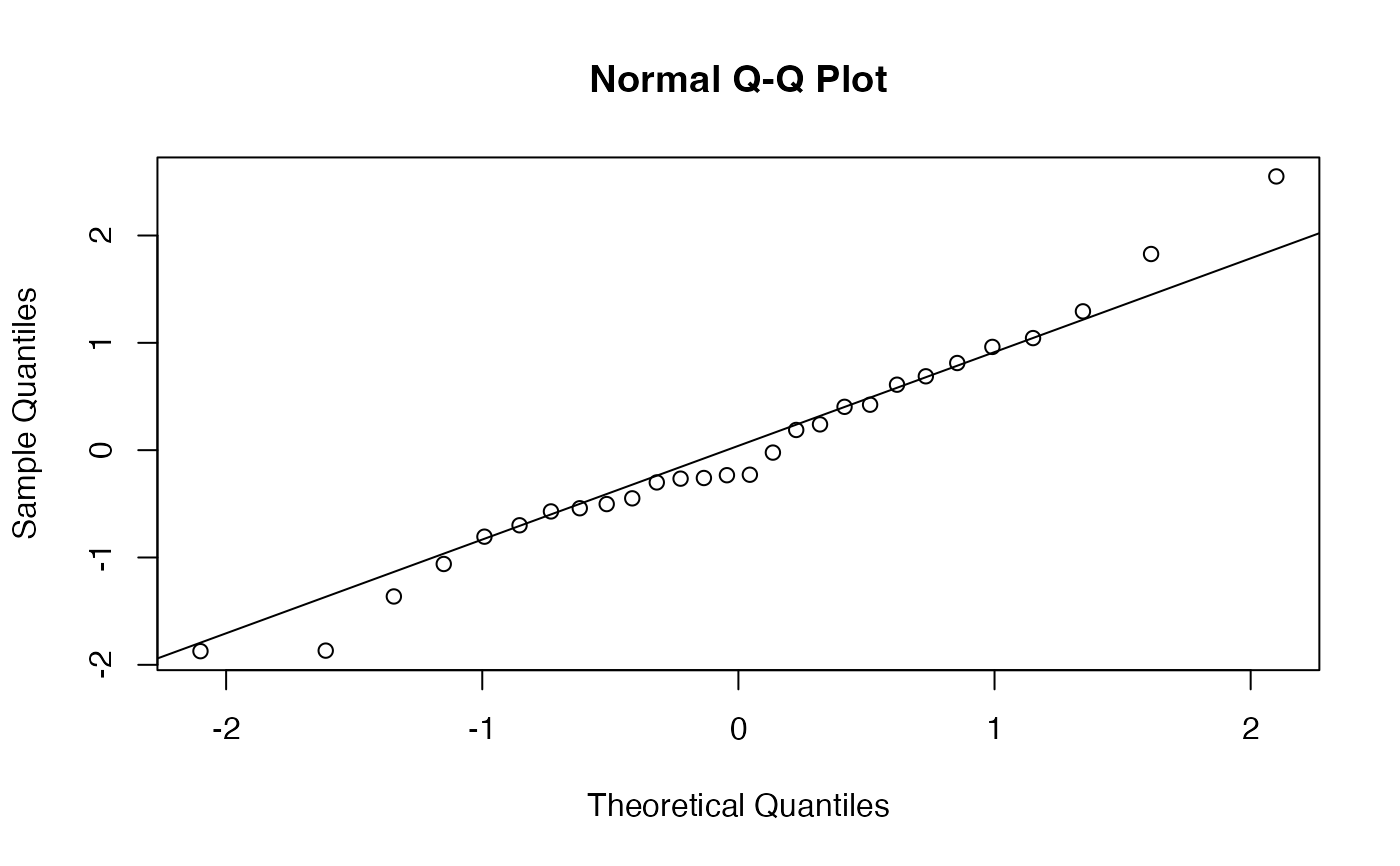
qq_plot

Logical. If TRUE, draws a QQ-plot of standardized increments to check model assumptions. Default is FALSE.

formatted

Logical. If TRUE, returns an "ext_di" object; otherwise returns a raw list. Default is TRUE.

digits

Integer. Preferred significant digits for printing. Affects display only. Default is getOption("extr.digits", 5).

Value

A list (class "ext_di" if formatted=TRUE) with:

  • Growth.rate, Variance, Unbiased.variance;

  • AIC;

  • Extinction.probability with confidence limits;

  • data summary (nq, xd, sample.size);

  • input parameters (unit, ne, th, alpha).

Details

Population dynamics follow $$dX=\mu\,dt+\sigma\,dW,$$ where \(X(t)=\log N(t)\), \(\mu\) is the growth rate, \(\sigma^2\) the environmental variance, and \(W\) a Wiener process. Extinction risk is $$G=\Pr[T\le t^{\ast}\mid N(0)=n_0,n_e,\mu,\sigma],$$ the probability the population falls below \(n_e\) within \(t^{\ast}\). Irregular intervals are allowed.

The function:

  1. estimates \(\mu\) and \(\sigma^2\) (Dennis et al., 1991),

  2. computes extinction probability \(G(w,z)\) (Lande and Orzack, 1988),

  3. constructs confidence intervals for \(G\) using the \(w\)-\(z\) method (Hakoyama, 2025).

Numerical range. Probabilities are evaluated on \(G\), \(\log G\), and \(\log(1-G)\) scales. The log-scale removes the \(\approx 4.94\times10^{-324}\) lower bound of linear doubles and extends the safe range down to exp(-DBL_MAX) (kept symbolically), avoiding underflow/cancellation.

References

Lande, R. and Orzack, S.H. (1988) Extinction dynamics of age-structured populations in a fluctuating environment. Proceedings of the National Academy of Sciences, 85(19), 7418–7421.

Dennis, B., Munholland, P.L., and Scott, J.M. (1991) Estimation of growth and extinction parameters for endangered species. Ecological Monographs, 61, 115–143.

Hakoyama, H. (2025) Confidence intervals for extinction risk: validating population viability analysis with limited data. Preprint, doi:10.48550/arXiv.2509.09965

See also

statistics_di, extinction_probability_di, confidence_interval_wz_di, print.ext_di

Author

Hiroshi Hakoyama, hiroshi.hakoyama@gmail.com

Examples

# Example from Dennis et al. (1991), Yellowstone grizzly bears
dat <- data.frame(Time = 1959:1987,
Population = c(44, 47, 46, 44, 46, 45, 46, 40, 39, 39, 42, 44, 41, 40,
33, 36, 34, 39, 35, 34, 38, 36, 37, 41, 39, 51, 47, 57, 47))

# Probability of decline to 1 individual within 100 years
ext_di(dat, th = 100)
#> --- Estimates ---
#>                                                       Estimate
#> Probability of decline to 1 within 100 years (MLE): 9.4128e-05
#> Growth rate (MLE):                                   0.0023556
#> Variance (MLE):                                        0.01087
#> Unbiased variance:                                    0.011273
#> AIC for the distribution of N:                          165.06
#>                                                                        CI
#> Probability of decline to 1 within 100 years (MLE):  (1.4586e-13, 0.5653)
#> Growth rate (MLE):                                  (-0.038814, 0.043525)
#> Variance (MLE):                                     (0.0070464, 0.020885)
#> Unbiased variance:                                                      -
#> AIC for the distribution of N:                                          -
#> 
#> --- Data Summary ---
#>                               Value
#> Current population size, nq:     47
#> xd = ln(nq / ne):            3.8501
#> Sample size, q + 1:              29
#> 
#> --- Input Parameters ---
#>                                                         Parameter
#> Time unit:                                                  years
#> Extinction threshold of population size, ne:                    1
#> Time window for extinction risk evaluation (years), th:     100.0
#> Significance level, alpha:                                   0.05

# Probability of decline to 10 individuals within 100 years
ext_di(dat, th = 100, ne = 10)
#> --- Estimates ---
#>                                                       Estimate
#> Probability of decline to 10 within 100 years (MLE):  0.096852
#> Growth rate (MLE):                                   0.0023556
#> Variance (MLE):                                        0.01087
#> Unbiased variance:                                    0.011273
#> AIC for the distribution of N:                          165.06
#>                                                                         CI
#> Probability of decline to 10 within 100 years (MLE):  (1.0699e-05, 0.9898)
#> Growth rate (MLE):                                   (-0.038814, 0.043525)
#> Variance (MLE):                                      (0.0070464, 0.020885)
#> Unbiased variance:                                                       -
#> AIC for the distribution of N:                                           -
#> 
#> --- Data Summary ---
#>                               Value
#> Current population size, nq:     47
#> xd = ln(nq / ne):            1.5476
#> Sample size, q + 1:              29
#> 
#> --- Input Parameters ---
#>                                                         Parameter
#> Time unit:                                                  years
#> Extinction threshold of population size, ne:                   10
#> Time window for extinction risk evaluation (years), th:     100.0
#> Significance level, alpha:                                   0.05

# With QQ-plot
ext_di(dat, th = 100, qq_plot = TRUE)

#> --- Estimates ---
#>                                                       Estimate
#> Probability of decline to 1 within 100 years (MLE): 9.4128e-05
#> Growth rate (MLE):                                   0.0023556
#> Variance (MLE):                                        0.01087
#> Unbiased variance:                                    0.011273
#> AIC for the distribution of N:                          165.06
#>                                                                        CI
#> Probability of decline to 1 within 100 years (MLE):  (1.4586e-13, 0.5653)
#> Growth rate (MLE):                                  (-0.038814, 0.043525)
#> Variance (MLE):                                     (0.0070464, 0.020885)
#> Unbiased variance:                                                      -
#> AIC for the distribution of N:                                          -
#> 
#> --- Data Summary ---
#>                               Value
#> Current population size, nq:     47
#> xd = ln(nq / ne):            3.8501
#> Sample size, q + 1:              29
#> 
#> --- Input Parameters ---
#>                                                         Parameter
#> Time unit:                                                  years
#> Extinction threshold of population size, ne:                    1
#> Time window for extinction risk evaluation (years), th:     100.0
#> Significance level, alpha:                                   0.05

# Change digits
ext_di(dat, th = 100, ne = 10, digits = 9)
#> --- Estimates ---
#>                                                           Estimate
#> Probability of decline to 10 within 100 years (MLE):  0.0968521443
#> Growth rate (MLE):                                   0.00235564171
#> Variance (MLE):                                       0.0108702457
#> Unbiased variance:                                    0.0112728474
#> AIC for the distribution of N:                          165.058678
#>                                                                                 CI
#> Probability of decline to 10 within 100 years (MLE):  (1.0698563e-05, 0.989801572)
#> Growth rate (MLE):                                   (-0.0388142081, 0.0435254915)
#> Variance (MLE):                                      (0.00704642493, 0.0208851222)
#> Unbiased variance:                                                               -
#> AIC for the distribution of N:                                                   -
#> 
#> --- Data Summary ---
#>                                   Value
#> Current population size, nq:         47
#> xd = ln(nq / ne):                1.5476
#> Sample size, q + 1:                  29
#> 
#> --- Input Parameters ---
#>                                                          Parameter
#> Time unit:                                                   years
#> Extinction threshold of population size, ne:                    10
#> Time window for extinction risk evaluation (years), th:      100.0
#> Significance level, alpha:                                    0.05